El estudio de escenarios base de diseño (DBS) es el elemento esencial del llamado análisis determinista de seguridad (DSA) de plantas nucleares. Se centra en la simulación, mediante modelos computacionales (también llamados códigos de cálculo) del comportamiento de las plantas durante los DBS. Es la autoridad reguladora nuclear quien define los escenarios y las cantidades físicas de seguridad que deben calcularse con los códigos, e impone los criterios de aceptación para esas cantidades calculadas (que llamaremos aquí criterios reguladores de aceptación, CRA). El DSA se basa en cálculos. Y todo cálculo, realizado con modelos predictivos y utilizando cantidades físicas, da lugar a resultados afectados por incertidumbre. En este artículo hablaremos del análisis de incertidumbre para los cálculos de escenarios base de diseño en centrales nucleares. 

Texto: Rafael Mendizábal Sanz | consejero técnico del Área de Ingeniería del Núcleo 

Los cálculos son esenciales en ciencia e ingeniería. Y es importante conocer la fiabilidad de sus resultados, su fidelidad a la realidad, que depende de dos cosas:  

• La calidad de los modelos computacionales, que tiene que ver con su capacidad para predecir la realidad analizada.
• La dificultad para conocer el valor real de los datos de entrada al cálculo

Estas limitaciones introducen incertidumbre en el cálculo; el calculista no tiene la seguridad de que sus resultados describan la situación real que intenta simular. La incertidumbre tiene su propia definición en ciencia. Así, se puede decir que la incertidumbre de una cantidad numérica es una representación matemática de la dispersión de los valores que se le pueden atribuir. La representación matemática tiene luego una traducción numérica; es decir, la incertidumbre se define matemáticamente, pero se calcula numéricamente. 

Clásicamente se distingue entre dos tipos de incertidumbre. Existen magnitudes físicas cuyo valor es difícil de conocer, porque exhiben una gran variabilidad; por ejemplo, en el tiempo y/o el espacio. Este tipo de incertidumbre se denomina aleatoria. Y existe, por otra parte, una incertidumbre atribuible al observador o usuario de la magnitud, a su desconocimiento o falta de información sobre su valor. Esta incertidumbre se denomina epistémica, y claramente es subjetiva, ya que depende del observador. Además, se puede reducir, a base de aumentar la información del observador, y por eso se la denomina a veces incertidumbre reducible. En contraste, la incertidumbre aleatoria es irreducible, porque un aumento de información no la puede rebajar.

En definitiva, la incertidumbre de una magnitud física representa la falta de fiabilidad en su valor, ya sea por su variabilidad o por el desconocimiento de su observador o usuario. 

Modelos e incertidumbre

Los modelos computacionales, también llamados códigos, producen resultados con incertidumbre. Un motivo básico es que los modelos son representaciones matemáticas simplificadas de la realidad física, y por tanto son imperfectos. Y por ello son inexactos: el valor calculado con un modelo de una magnitud física no coincide, en general, con su valor real, sino que existe un sesgo o error. Los sesgos no se pueden conocer a la perfección; de lo contrario, permitirían una predicción exacta de la realidad; o sea, un modelo perfecto. Por tanto, el conocimiento imperfecto del error del modelo produce incertidumbre epistémica en sus resultados.

Por otra parte, los modelos transforman variables de entrada en resultados. Las variables de entrada pueden, y suelen, tener incertidumbre. Operar con datos inciertos lleva a resultados inciertos. Se dice que la incertidumbre de las variables de entrada se propaga, a través del modelo o del cálculo, a los resultados.

En definitiva, son los modelos y sus variables de entrada las dos fuentes básicas de la incertidumbre de las cantidades calculadas. 

Modelos deterministas y aproximación de caja negra

Todo modelo o código de cálculo define una correspondencia input-output. En lenguaje matemático, se trata de una correspondencia desde un espacio de entrada a otro de salida. Cada punto en el espacio de entrada representa un posible conjunto numérico de entrada al código (en inglés input deck), que, alimentado al código, produce un cálculo cuyo resultado es un punto del espacio de salida (figura 1). 

Aquí trataremos de los modelos y códigos denominados deterministas, que cumplen la condición de que, aplicados a un punto concreto del espacio de entrada, dan siempre como resultado un mismo punto del espacio de salida. Esta propiedad de repetibilidad puede parecer trivial, pero no lo es tanto, porque existen modelos que incluyen el uso de números aleatorios, de forma que los resultados pueden variar de un cálculo a otro, aunque el conjunto de entrada sea el mismo. 

En matemáticas, una correspondencia entre conjuntos que asigna a cada punto origen un solo punto imagen se denomina aplicación o función. Por tanto, todo modelo determinista tiene asociada una función numérica input-output.

Cuando un modelo determinista se identifica con su función input-output asociada, se dice que hay una “aproximación de caja negra” al modelo. En este artículo contemplamos los modelos deterministas como cajas negras. No significa este enfoque que haya un desconocimiento real de los modelos; es decir, de su estructura matemática, sus ecuaciones o algoritmos asociados. Simplemente, no se utiliza ese conocimiento, o se hace mínimamente, a la hora de realizar el análisis de incertidumbre.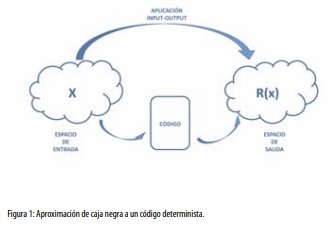  

Metaincertidumbre

Hemos visto que toda cantidad calculada tiene incertidumbre, que surge del modelo de cálculo y de sus variables de entrada. Pero la incertidumbre también se debe modelar y calcular, y eso significa que, una vez modelada y calculada, también es un magnitud incierta [4]. Existe, por tanto, la incertidumbre de la incertidumbre, un concepto al que cuadra bien el término metaincertidumbre, aunque a veces se utiliza el menos imponente de incertidumbre de segundo nivel. De ella hablaremos más adelante. 

Existen varias maneras de modelar matemáticamente la incertidumbre. Dos maneras clásicas, utilizadas ambas en seguridad nuclear, son las distribuciones de probabilidad y los intervalos o regiones. En el primer método, la cantidad numérica incierta se considera una variable aleatoria, y la incertidumbre se identifica con la distribución de probabilidad. 

Menos sofisticada es la modelación de la incertidumbre con intervalos o regiones numéricas. En este caso, la cantidad incierta se describe mediante una región que engloba sus posibles valores. Para variables escalares, esa región es típicamente un intervalo numérico, y para variables multidimensionales es una región también multidimensional.  

La forma de modelar la incertidumbre también se propaga a través del cálculo. Si se modela mediante distribuciones de probabilidad, su propagación da lugar a distribuciones de probabilidad de los resultados; si se modela mediante regiones, su propagación produce regiones para los resultados.

Representación probabilista de la incertidumbre 

En las metodologías tradicionales (llamadas conservadoras) de análisis de accidentes de la seguridad nuclear, la modelación de la incertidumbre se realiza mediante intervalos unilaterales. A los parámetros de entrada que son significativamente influyentes en los resultados de seguridad se les asigna un valor numérico pesimista, de acuerdo con la severidad del resultado. Típicamente, incluso, se recurre a valores “muy pesimistas”, con lo que se obtienen resultados también muy pesimistas. El objetivo es sobrestimar la incertidumbre del resultado para tener gran certeza de que cubre los valores de hipotéticos accidentes reales. La propagación de la incertidumbre es aquí muy sencilla; en esencia, se hace un cálculo con las variables inciertas en sus valores pesimistas y el resultado se compara con los límites de aceptación definidos por el regulador. 

Las metodologías conservadoras fueron necesarias cuando la fenomenología de los escenarios base de diseño no se conocía en profundidad y los modelos eran necesariamente simples y, a veces, bastante empíricos. Cuando el conocimiento experimental de la fenomenología y la capacidad teórica y computacional aumentaron lo suficiente, se abrió la puesta al uso de modelos predictivos realistas (llamados también best estimate) en el análisis de accidentes [1]. Las metodologías basadas en cálculos con estos códigos, suplementados por el análisis de incertidumbre de sus resultados, se denominan BEPU (BestEstimate Plus Uncertainty), y suponen un importante avance con respecto a las metodologías conservadoras. La gran mayoría de las metodologías BEPU existentes son probabilistas, y a veces se designan como metodologías estadísticas. 

¿Cómo se analiza la propagación a través de un cálculo de la incertidumbre descrita por distribuciones de probabilidad? El procedimiento clásico es el método de Monte Carlo. En esencia, se obtienen muestras aleatorias de los parámetros inciertos, a partir de sus distribuciones de probabilidad. Alimentando el modelo con los sucesivos conjuntos de entrada se obtiene la correspondiente muestra aleatoria de los resultados del código, a partir de la cual se estiman, mediante técnicas estadísticas, sus distribuciones de probabilidad (figura 2). 

La estadística es el arte de estimar distribuciones de probabilidad a partir de muestras aleatorias. Éstas tienen, obviamente, tamaño finito y dan una información incompleta sobre la distribución de origen; por ello, las estimaciones estadísticas tienen incertidumbre y existe un término clásico bien conocido para describirla: la confianza estadística. Esta, recordando un término introducido previamente, describe un tipo de metaincertidumbre. 

Criterios de aceptación con incertidumbre 

Los criterios reguladores de aceptación (CRA) son condiciones que deben cumplir los resultados de los análisis deterministas de seguridad. Los escenarios base de diseño (DBS) se clasifican en categorías, y, para cada una de ellas, la autoridad reguladora establece los resultados de seguridad que tienen que calcularse y sus criterios reguladores de aceptación (CRA). El cumplimiento de los criterios implica que las consecuencias de los DBS no producen daños inaceptables. Lógicamente, los CRA deben tener en cuenta, en su formulación, la incertidumbre de cálculo de los resultados de seguridad, y la manera en que se modela. 

Supongamos que en el análisis DBS se calcula un resultado de seguridad V escalar, continuo y con valores positivos, y tal que, a mayor valor de V, más severas las consecuencias del escenario. Entonces, el regulador impone sobre la V calculada un límite superior de aceptación L. Para metodologías tradicionales, la forma del CRA para V es, por tanto:  VC < L

El subíndice C en (1) indica que V se ha calculado de manera conservadora. 

Cuando se utiliza una metodología BEPU probabilista, el resultado V se modela como una variable aleatoria y el criterio de aceptación se hace probabilista, de la forma

PRV{V < L} ≥ P0

En el primer miembro de (2) aparece la probabilidad (que aquí tiene el sentido de “certidumbre”) de que V sea menor que L, calculada con la distribución de probabilidad de V. El criterio establece que dicha probabilidad es grande, porque P0 es un valor de probabilidad cercano a 1, establecido también por el regulador, y llamado nivel regulador de probabilidad. El valor estándar de P0 es 0.95. 

La forma (2) se puede simplificar, recurriendo al concepto de cuantil de una variable aleatoria. Para la variable aleatoria continua V, el cuantil de orden P (donde P es un valor real comprendido entre 0 y 1) es el valor VP de la variable tal que la probabilidad de que V esté por debajo de VP es P. Es obvio que, cuanto más grande es P (más cercano a 1), más grande es el valor VP dentro de la población. 

Utilizando el concepto de cuantil, (2) se puede reescribir como VP0 < L

Así que la introducción de la incertidumbre probabilista conlleva sustituir un valor conservador de V (con conservadurismo no cuantificado, pero que se considera “suficiente”) por un cuantil de orden alto y conocido de la cantidad. 

En (3) está la incertidumbre de cálculo, pero no “toda” la incertidumbre. Es un hecho que, en general, no se conoce a la perfección la distribución de probabilidad de V, porque la propagación de incertidumbre a través del modelo se hace de forma parcial. El procedimiento típico de propagación es la técnica de Monte Carlo, de manera que, en la aproximación de caja negra, todo lo que se conoce de V es una muestra finita de valores; a partir de ella, lo más que puede obtenerse son estimaciones estadísticas de su distribución de probabilidad. Las estimaciones tienen una incertidumbre estadística, que es la incertidumbre de segundo nivel de V, de carácter epistémico. 

Si una distribución de probabilidad es incierta, también lo es cualquier cantidad calculada a partir de ella. Es decir, tanto la probabilidad que aparece en el primer miembro de (2) como el cuantil que figura en (3) son, en ese caso, cantidades inciertas. Esta incertidumbre de segundo nivel puede modelarse de varias maneras; por ejemplo, mediante intervalos o distribuciones de probabilidad. En este último caso, se añade a (2) una segunda “capa” de incertidumbre, en la forma PRS {PRV{V < L} ≥ P0 } ≥ C0

Si, como es frecuente, la propagación de incertidumbres se hace mediante un análisis de Monte Carlo puro, se obtiene una muestra aleatoria simple (MAS) de valores de V. En ese caso, la probabilidad en (2) o el cuantil en (3) tiene distribuciones ligadas al proceso de muestreo (sampling en inglés, de ahí el subíndice S en (4)), y la probabilidad externa en (4) se denomina confianza, un término clásico en estadística. 

También C0 es un valor alto de probabilidad (cercano a 1), establecido por el regulador (con valor estándar de 0.95) y denominado nivel regulador de confianza. El par (P0 , C0 ) se denomina nivel regulador de tolerancia estadística. Su valor estándar es (0.95, 0.95) y, con él, los criterios de aceptación se califican de “criterios 95/95”. (4) no tiene una forma sencilla, con dos probabilidades anidadas. Su escritura es complicada, pero se lee con facilidad, como “V es menor que L con probabilidad mayor o igual a P0 y confianza mayor o igual a C0 ”

(4) se puede simplificar, utilizando de nuevo los cuantiles de V tadística traduciría (5) como sigue: un límite superior PRV{VP0 < L } ≥ C0

Alguien experto en estadística traduciría (5) como sigue: un límite superior de confianza de nivel C0 del cuantil P0 de V debe ser menor que L. O diría, equivalentemente, que un límite superior de tolerancia de nivel (P0 , C0 ) de V debe ser menor que L, expresado como:  V (P0,C0) < L.

Los criterios (1), (3) y (6) tienen complejidad creciente, debido a la introducción de los dos niveles de incertidumbre. En (1), la figura de mérito (FOM) que se compara con L es un valor conservador de V; en (3) es un cuantil de orden alto de V, y en (6) la FOM es un límite superior de confianza, de nivel alto, del citado cuantil. Se puede decir que las expresiones (4)-(6) representan el criterio regulador de aceptación para metodologías BEPU. 

La confianza estadística aparece en el CRA debido al tamaño finito de la muestra disponible de valores de V. Si aumenta el tamaño, la incertidumbre de segundo nivel decrece, y puede hacerse despreciable para tamaños muy grandes. En ese caso límite, la distribución de probabilidad de V y el correspondiente cuantil de orden P0 se pueden conocer con gran precisión, y el CRA tiene las formas (2)-(3). Esta posibilidad se da cuando los cálculos con el código consumen muy poco tiempo (y otros recursos) de ordenador, y se pueden realizar de manera masiva.  

Verificación del cumplimientos de un criterio de aceptación.

El paso definitivo del análisis BEPU de un DBS es la comprobación del cumplimiento del criterio regulador de aceptación. Si se cumple, hablamos de “diseño seguro”. Si no se satisface, el diseño de seguridad debe modificarse hasta que se verifique el cumplimiento. 

¿Cómo se hace esta comprobación? Es fácil cuando el criterio tiene la forma (3), porque basta con generar una muestra aleatoria muy grande de valores de V, calcular a partir de ella , de forma trivial, el cuantil de orden P0 y compararlo con el límite L.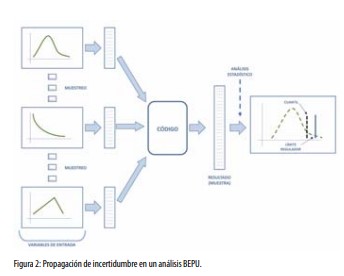 

Cuando la incertidumbre de segundo nivel no se puede despreciar, el criterio toma la forma (6). La comprobación se hace, entonces, calculando un límite superior de tolerancia de nivel (P0 , C0 ) y comparándolo con L. Este procedimiento es un caso particular del llamado “método de los intervalos de tolerancia” para comprobar (6). Dada la variable aleatoria V, una MAS de V de tamaño N y dos números reales P y C comprendidos entre 0 y 1, se define un intervalo de tolerancia IT de nivel (P, C) de V como un intervalo en el rango de V tal que un nuevo valor de V (independiente de la MAS) está contenido en IT con probabilidad mayor o igual a P y confianza estadística mayor o igual a C [3]. 

Llamemos intervalo de aceptación de V al conjunto de sus valores que están por debajo del límite regulador L. El método de los intervalos de tolerancia para comprobar (6) se basa en el siguiente resultado. Si, a partir de una MAS, se construye un intervalo de tolerancia para V de nivel regulador (P0 , C0 ), y dicho intervalo resulta estar contenido en el intervalo de aceptación de V, entonces se cumple el criterio de aceptación (6). Los intervalos de tolerancia pueden ser uni o bilaterales. La desigualdad (6) viene a decir que un intervalo unilateral de tolerancia de nivel (P0 , C0 ) está contenido en el intervalo de aceptación de V.

La diferencia básica entre la comprobación de los criterios (3) y (6) es que, en el primer caso, la figura de mérito (FOM) que se compara con el límite L es un cuantil de V, una cantidad fija que solo depende del código y de las distribuciones de probabilidad de las variables de entrada. Y, en el segundo caso, la FOM es un límite de tolerancia, que depende también de esos dos elementos y, además, de la muestra aleatoria utilizada. Si cambia la muestra, cambia la FOM. 

En consecuencia, para verificar el cumplimiento de un CRA son necesarios métodos de cálculo de intervalos de tolerancia y métodos de estimación de cuantiles por intervalos. Existen muchas clases de procedimientos estadísticos de este tipo; aquí nos centraremos en el conocido como método de Wilks. 

El método no paramétrico de Wilks  

El matemático tejano Samuel S. Wilks (1906-1964) fue uno de los más más notables estadísticos de la primera mitad del siglo XX. Una de sus principales aportaciones la desarrolló en respuesta a un requerimiento formulado por Walter A. Shewhart (el creador del control estadístico de calidad en procesos de fabricación), y fue el desarrollo, en 1941, de su método no paramétrico para construir intervalos estadísticos de tolerancia [8, 9]. Este método ha constituido una técnica muy conocida y aplicada. A finales de la década de 1980, la organización alemana GRS comenzó a utilizarlo en los análisis BEPU de termohidráulica nuclear [2]. A partir de ahí, el método comenzó a aplicarse masivamente en el análisis de incertidumbre de cálculos de seguridad nuclear, basándose en MAS de resultados de los cálculos. Los intervalos que genera son “libres de distribución” (distribución free en inglés), también llamados no paramétricos, significando que el procedimiento de construcción es el mismo cualquiera que sea la distribución de la variable aleatoria en cuestión. 

El método de Wilks se basa en muestras aleatorias simples (MAS), y utiliza como extremos de los intervalos de tolerancia los llamados estadísticos de orden (OS), un concepto de definición sencilla. Se parte de una variable aleatoria V continua y escalar y con la llamada función de distribución acumulada (cdf) continua. Dada una MAS de tamaño N de V, sus elementos pueden ordenarse de menor a mayor, y entonces se les asigna un subíndice que representa su ordinal: V(1) < V(2) < …..< V(N-1) < V(N). Por tanto, V(1) y V(N) son, respectivamente, el mínimo y máximo muestral; V(2) y V(N-1) son el segundo mínimo y segundo máximo de la muestra y así sucesivamente. 

El método de Wilks permite construir tanto intervalos unilaterales, con extremo en un OS (llamado límite inferior o superior de tolerancia, según el caso) como bilaterales (delimitados por dos OS). Para cada una de esas modalidades existe una fórmula de Wilks diferente, dando lugar a tamaños mínimos de muestra que, a igualdad de otros factores, son menores para la modalidad unilateral que para la bilateral.

En definitiva, el método de Wilks permite hacer una propagación de incertidumbre de menor coste computacional que un análisis convencional de Monte Carlo. Para ello, utiliza tamaños moderados de muestra, que no permiten obtener con precisión la distribución de probabilidad de los resultados, pero sí construir intervalos de tolerancia para ellos, suficientes para comprobar el cumplimiento de los CRA.

La gran aceptación del método de Wilks se debe a su simplicidad y a su mínimo número de hipótesis [5]. Es un método frecuentista, que no necesita establecer ni justificar una distribución prior. Es método exacto, así que no tiene que justificar ninguna aproximación. Es libre de distribución y, por tanto, no necesita demostrar que la población sigue una distribución paramétrica específica. Además, se basa en un MAS del modelo o código original, con lo que no necesita otros tipos de muestreo, ni la construcción de ningún metamodelo o emulador. 

Incluso uno de los defectos del método de Wilks, que es su poca eficiencia (es decir, una significativa variabilidad de sus estimadores), puede resultar una ventaja a ojos del regulador, porque tiende a dar resultados más conservadores que otros métodos de estimación de cuantiles. 

Aún así, se han aplicado numerosos métodos alternativos al de Wilks, que pueden encontrarse en la literatura estadística. Los hay paramétricos y no paramétricos, aproximados y exactos, frecuentistas y bayesianos, basados en MAS o en otros tipos de muestreo. Algunos hacen la propagación de incertidumbre a través del código original, y otros la hacen a través de modelos sustitutivos simplificados (llamados también metamodelos). 

El problema multivariante

Se ha descrito en detalle el análisis de incertidumbre de la situación más sencilla: una sola cantidad escalar y continua, sujeta a un criterio de aceptación. Sin embargo, no es raro que un DBS tenga asociadas varias cantidades escalares de seguridad, cada una sometida a su CRA. Este es un problema multidimensional o, en lenguaje estadístico, multivariante. Los conceptos de intervalo de aceptación e intervalo de tolerancia son fácilmente generalizables a regiones de varias dimensiones [3]. Para verificar el cumplimiento simultáneo de múltiples CRA escalares, se utiliza el método de regiones de tolerancia, extensión del método de intervalos de tolerancia, citado previamente. Si se construye, a partir de la MAS multivariante, una región de tolerancia de nivel regulador y ésta resulta estar contenida en la región de aceptación, se concluye el cumplimiento de los criterios de aceptación con el nivel regulador de tolerancia. 

El método de Wilks es aplicable sólo a variables aleatorias escalares, pero el matemático húngaro Abraham Wald publicó en 1943 una extensión del método a variables multivariantes, que permite construir regiones de tolerancia multidimensionales no paramétricas mediante estadísticos de orden [7].

No obstante, la extensión de Wald no es el único procedimiento para tratar el problema multivariante. El método de Wilks se puede aplicar al problema. Basta con hacer un adecuado cambio de variables, que transforme la cantidad multidimensional en una escalar, y aplicar a ésta el método de Wilks. El límite de tolerancia obtenido se convierte, mediante la transformación inversa, en una región de tolerancia multidimensional [6]. Esto significa, además, que el problema multivariante se puede reducir al sencillo problema escalar que hemos descrito en este artículo. 

Epílogo: Licenciar con probabilidades… 

Cuando se utilizan metodologías BEPU, el análisis determinista de accidentes adquiere carácter probabilista. El regulador decide el nivel de tolerancia estadística para el cumplimiento de los criterios de aceptación. El valor estándar de (95, 95) significa que se permite una probabilidad de hasta 0.05 de que no se cumpla el CRA, con confianza 0.95 ¿Es suficiente el uso del nivel estándar, o el regulador debería imponer valores más altos? 

En la elección del nivel regulador de tolerancia deben ser claves los conservadurismos que lleva aparejado el DSA. Para empezar, los DBS se establecen para maximizar sus consecuencias negativas, de forma que cubran las de cualquier escenario de accidente dentro de su categoría. Por otra parte, los límites reguladores de aceptación se establecen también de manera pesimista, para asegurar un margen notable hasta el verdadero umbral de daño a la correspondiente barrera de seguridad. Y, además, las metodologías BEPU no son puramente realistas, sino que contienen un cierto número de conservadurismos. El regulador puede permitir un nivel de tolerancia no excesivamente alto a cambio de la existencia de otros márgenes de seguridad significativos. 

…y con números aleatorios

La suficiencia de los niveles de tolerancia no es el único problema regulador que plantea el uso de las metodologías BEPU. Están, además, las implicaciones de utilizar métodos estadísticos. En este artículo hemos comprobado que la figura de mérito (FOM) que se compara con límites reguladores se construye a partir de una muestra aleatoria de valores de la cantidad; si cambia la muestra cambia el valor de la FOM. Así que este valor de licencia es, en puridad, un número aleatorio, el resultado de un sorteo. Si la FOM no cumpliera el criterio de aceptación, alguien podría tener la idea de probar fortuna con otra muestra, y esa acción invalidaría el análisis de seguridad. 

Por ello, el regulador debe controlar el proceso de generación de la muestra aleatoria. Típicamente, para obtener una muestra se utilizan generadores de números pseudoaleatorios, que obtienen secuencias de números deterministas que emulan números aleatorios. Cada secuencia parte de una semilla numérica; si se repite ésta, se repite la muestra. A su vez, la semilla se elige de una manera automática, o se introduce arbitrariamente. El regulador debe cerciorarse de que la elección de semilla no está dirigida a obtener una muestra favorable, y lo puede hacer, por ejemplo, imponiendo su valor, o comprobando que el valor proviene de un proceso automático no controlado por el analista. 

No sabemos si Shakespeare pudo presagiar esta relación del análisis de seguridad con una “semilla” cuando hizo exclamar al rebelde Hotspur…but I tell you, my lord fool, out of this nettle, danger, we pluck this flower, safety.